In Defense of Conditional Excluded Middle
The rule of excluded middle says that for any proposition P, P is either true or not-true (and not both). The "or" here is exclusive because otherwise P and not-P could be true at the same time, which would violate the law of non-contradiction.
Similar to excluded middle is a controversial rule known as conditional excluded middle (CEM) which may be stated as follows:
(CEM) For all propositions P and Q, if P then (either Q or not-Q).
Again, the "or" is exclusive. Given CEM, either "If P then Q" is true or "If P then not-Q" is true, and not both. We may not know which one is true, but we can be sure that one, and only one, of them is true.
Now I think CEM is true. It seems so intuitively obvious to me that I find it very hard to see how it could be false. Nevertheless, CEM is controversial. David Lewis has offered the following counterexample:
- If Verdi and Bizet were compatriots, Bizet would be Italian.
- If Verdi and Bizet were compatriots, Bizet would not be Italian.
The standard sort of response to Lewis is to question whether (1) is just as likely to be true as (2) by considering the relative similarity of possible worlds to the actual world. I think that sort of response is unlikely to be effective because our modal intuitions about which worlds are closer to the actual world are likely to be highly variable and unreliable.
Here's what I think the defender of CEM should say: Both (1) and (2) are false.
But wait a minute! Isn't that self-defeating? Am I giving up CEM in the process of defending it? The answer is emphatically no. I can uphold CEM while denying both (1) and (2) because I deny that the consequents of (1) and (2) are contradictories. The denial of the consequent of (1) gives us not (2) but
- If Verdi and Bizet were compatriots, then it is not the case that Bizet would be Italian.
- If Verdi and Bizet were compatriots, then it is not the case that Bizet would not be Italian.
- If Verdi and Bizet were compatriots, then it is neither the case that Bizet would be Italian nor the case that Bizet would not be Italian.
- If Verdi and Bizet were compatriots, then Bizet might and might not be Italian.
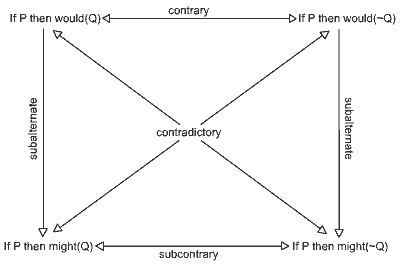
If this is right, then the top two corners of the square are false just in case both bottom corners are true, and Lewis's counterexample to CEM fails.

11 Comments:
This seems a bit wired, or perhaps just trivial, to me:
(EM): For any proposition P, P is either T or F [essentially (either P or no-P) for all propositions]
And then:
(CEM): For all propositions P and Q, if P then (either Q or not-Q).
Seems to me one can argue that CEM is either trivial or not always the case.
First, (either Q or not-Q) just is (EM). So CEM reduces to:
(CEM): If P then (EM)
which is trivially true. It amounts to saying:
If P then God exists (for theists at least!)
Or
If P then 2 + 2 = 4
which is trivially true.
Secondly, I’m still trying to understand just what relationship is posited by “If…then” propositions. Presummably is posits something non-trivial. So (CEM) then says more than just
If P then (EM)
But I don’t see what that might be. If it’s being claimed that some causal relationship obtains, then CEM is obviously false, since (EM) isn’t true because P is true. P’s truth value (if contingent) has nothing to do with the truth of (EM). But what else do we have in mind when we posit “If..then” props? I don’t get it.
Tom
Pardon all my typos! A bit 'weird' was what I mean. And others too!
Tom
Hi Tom,
Thanks for the input.
Regarding EM, be careful not to conflate it with bivalence (BV). BV says that, for all P, either P is true or P is false. EM says that, for all P, either P is true or not-P is true. These are not equivalent because if BV is false, then the truth of not-P does not imply the falsity of P. Instead, P might be neither true nor false.
As for CEM, I do think it is, or should be, a platitude. Hence it would be trivial if it were not for the case that it has been contested. And the reason it has been contested, I think, is because it has been applied in the wrong way to subjunctive conditionals. Nearly everyone seems to take it for granted that "If P then not-would(Q)" is equivalent to "If P then would(not-Q)". That's what I deny, and I think you do too: Remember will, will not, might & might not? Same thing.
Regarding, your examples "If P then God exists" and "If P then 2+2=4". These are trivially true given that both consequents are necessary and either material or strict implication are in view. On a relevance interpretation of the conditional, both are false for most P. By extension, on a relevance interpretation of the conditional CEM is also false, unless we take the somewhat radical route of introducing an analog of the would/would not/might & might not distinction into indicative conditionals.
Hmmm. You've given me something to think about. Perhaps someone attracted to relevance logic, as I am, should deny CEM for indicative conditionals and affirm it for subjunctive conditionals. In that case maybe we could even use CEM as a test for whether a conditional is indicative or subjunctive.
Good stuff, bro!
Alan,
You raise a very interesting and complicated issue in the logic of conditionals. May I ask a few questions and offer a few comments?
(a) Speaking now NOT in terms of formal relevance logics a la Anderson and Belnap, but in terms of ordinary speakers using English conditionals, I have a hard time hearing a ordinary speaker uttering an instance of “if p, then q or not q” on any interpretation of “if”, and certainly not on the sufficient condition meaning you regard as central.
Do you have any examples you like and would explain to me?
(b) I agree with your assessments of (1)- (5), with one proviso. English really wants the pluperfect forms in a counterfactual construction. The so-called “past” subjunctive forms ( were, were to ) mean something different. Thus, (1) should be
(1)* If (we suppose) that V and B had been compatriots ( in some fashion), B would have been Italian.
And that clearly does not follow, because our counterfactual stipulation or hypothesis ( they are compatriots ) simply does not address in what fashion they are supposed to be compatriots. Here is no “closer” ( French) or more “remote” ( Russian) case at this point. The question is simply open.
Likewise for (2)
I would rewrite (3) as
(3)* If (we suppose) that V and B had been compatriots ( in some fashion), it would not follow that B would have been Italian.
I agree, and similarly for (4).
(6) puzzles me because of “might and might not”. It is too long a story to raise here, so let me just ask, do you mean
(6)* If (we suppose) V and B had been compatriots ( in some fashion), it would remain open/possible that B would have been Italian, and it also would remain open/possible that would not have been Italian.
I accept (6)*.
( c ) I agree of course that Lewis has no counterexample to an indicative or counterfactual form of the CEM, but that fact still leaves me looking a few good examples to persuade me that “ if p, then q or not “ means anything in ordinary English.
Alan: Regarding EM, be careful not to conflate it with bivalence (BV).
Tom: Right. I was aware of that, which is why your definition of (EM): “The rule of excluded middle says that for any proposition P, P is either true or not-true (and not both)” was a bit confusing. This sounded to me more like BV (on the assumption that not-true = false). In any case, I take EM to be: For all P (P v not-P).
So when you define (CEM) as:
For all propositions P and Q, if P then (either Q or not-Q),
It looks to me like this reduces to:
For all propositions P and Q, if P then (EM) [since EM = (P v not-P) which is equivalent to (Q or not-Q)]
Alan: Nearly everyone seems to take it for granted that "If P then not-would(Q)" is equivalent to "If P then would(not-Q)". That's what I deny, and I think you do too: Remember will, will not, might & might not?
Tom: For sure. I’m with ya on this. I guess it’s conditionals in general I still struggle with.
Alan: Regarding, your examples "If P then God exists" and "If P then 2+2=4". These are trivially true given that both consequents are necessary and either material or strict implication are in view. On a relevance interpretation of the conditional, both are false for most P. By extension, on a relevance interpretation of the conditional CEM is also false, unless we take the somewhat radical route of introducing an analog of the would/would not/might & might not distinction into indicative conditionals…
Hmmm…
Tom: Yes! Hmmmm!
Alan: You've given me something to think about. Perhaps someone attracted to relevance logic, as I am, should deny CEM for indicative conditionals and affirm it for subjunctive conditionals. In that case maybe we could even use CEM as a test for whether a conditional is indicative or subjunctive.
Tom: Hmmm. I see an article in your future!
Tom
Phil,
I accept your revised statements of (1)-(6). Thanks for the extra precision.
As for a natural language example of "If P then (either Q or not-Q)" I don't have any conversational examples to offer. However, it doesn't seem far-fetched to me to imagine a person deliberating, as in a chess game, and saying to themselves, "If I move my bishop there, then either he takes my bishop or he doesn't. If he takes my bishop then ..."
Regards,
Alan
Alan,
Yes, absolutely, someone could reason that way in a chess game. What strikes me at once, though, is that the consequent of your conditional seems really to be a modal proposition, describing alternative possibilities of play created by supposing you make the move stipulated in the antecedent. If you expose your bishop, your opponent CAN THEN choose to capture it or do something else.
You don’t say, for example, “If I expose my bishop at that position, then it’s mate in five moves”. You say, “If I expose my bishop at that position, he can then capture it on the next move or decline to capture it.”
Suppose I’m thinking about offering a junior associate in our firm a partnership. I reason: “If I offer him the partnership, he can accept or decline it. If he accepts,…, whereas if he doesn’t accept….” That kind of reasoning is quite ordinary.
But doesn’t this kind of example really suggest how implausible the CEM is as an axiom supposed to apply to ANY propositions p and q? We see here the connection between p and q needed to make sense of the conditional. These example works just in case p is a supposition that creates the possibility of then doing or declining q . “If I expose my bishop, then he can bake a cake or not” even more clearly nonsense.
(If this doesn't help, please don't trouble yourself to reply.)
Phil,
I agree with you. For indicative conditionals we expect that the antecedent will be relevant to the consequent. If it isn't, as in your “If I expose my bishop, then he can bake a cake or not” example, then we judge the resulting conditional to be either nonsense or false. So CEM seems to fail for at least some indicative conditionals (unless we adopt a more lenient interpretation of the conditional a la material or strict implication).
I do think, however, that CEM holds for all subjunctive conditionals, the reason being that here our beliefs about the consequent naturally divide up into three modalities: would, would not, and might and might not. Whenever irrelevance renders the first two false, the third option remains as a catch-all.
Alan,
I think that we use subjunctive conditionals in English for two main purposes.
(1) We speak counterfactually about the past, the present or the timeless conditions:
a. “If I had been living in Arizona in 1990, I would have….”
b. “If I were living in California right now, I would…”
c. “If the square root of two were rational, then there would be a ratio n/m..…”
(2) We refer to possibilities about the past, present or future that we regard as dubious if not demonstrably false:
a. “If Homer did write the Odyssey, I would….”
b. “If it should turn out to be the case that the account is now empty, I would immediately….”
c. “If I were to attend the Dean’s party next week, I would not take Mary.”
All the usages in (2) can be, and increasingly are, being paraphrased in contemporary English by non-subjunctive constructions, in which the speaker’s doubt about the supposition is registered explicitly in an adjunct clause. So, in place of (2a) and (2c), we hear
(2a*) “If Homer wrote the Odyssey , which I doubt, I will…”
(2c*) “ If I attend the Dean’s party, which I don’t think I will, then I will not…”
It is going to be difficult to concede that the CEM fails for indicative conditionals but argue that it works for (2), ie, dubious-supposition subjunctives, given that that this whole usage is rapidly being absorbed into and paraphrased by indicative conditionals.
That leaves counterfactual conditionals ( cf’s).
You say you want to focus on cfs with a “might and/or might not” auxiliary in the consequent. It strikes me in general that cfs have an equally strong, or even stronger, requirement of relevance than do indicative conditionals. Shifting from “would have” to “might have” makes no difference on this score. ( But maybe you have some examples to the contrary?)
I’m thinking of sentences like
(3) “If I had sacrificed my rook on move 32, he might or might have baked a cake.” [ nonsense]
(4) “If the square root of two were rational, then it might or might rain tomorrow.” [ nonsense]
We can of course say something like
(5) "If I had sacrificed my rook on move 32, I might or might not have won.”
That means, I take it, that I regard the sacrifice as inconclusive to the outcome of the game. But then usage in (5) is patently another argument against the CEM for cf conditionals: (5) makes sense just in case we regard the antecedent’s condition as stating something that might have been decisive for the consequent but turns out not to be. A strong relevance condition.
Very interesting comments, Phil. I gather that you know more about this subject area than I do. That's great. I'm eager to learn. I've been slowly gathering books on conditionals over the last two years but still haven't read most of them. Looks like I'm gonna have to get started.
Anyway, my views about CEM derive from thinking about a couple particular classes of subjunctive conditionals: (a) so-called "counterfactuals of creaturely freedom" (CCF's), which figure prominently in philosophy of religion discussions about Molinism; and (b) ones expressing the causal dependence of one state of affairs on an earlier state of affairs. I think CEM holds for these cases.
What you're opening my eyes to is the fact that those may be just a subset of subjunctive conditionals, in which case my defense of CEM may have even narrower scope than I'd initially thought. If that turns out to be the case, I'm fine with that.
I'm not as inclined as you, however, to see your (3) and (4) as nonsense. (Minor aside: "might OR might not" is trivially applicable to anything; "might AND might not", however, expresses contingency, which is not trivial.) I can imagine a (possibly deluded) person thinking that there really is some relevance between sacrificing a rook on move 32 and whether or not someone else bakes a cake. In some cases there might actually be such a connection, e.g., I know that two people have made a bet that I'll move a rook on move 32 with the loser agreeing to bake a cake for the other. But on the assumption that the speaker is just deluded in thinking there's a connection, I want to say that the claim is meaningful but false. Similarly for (4).
So I agree with your point about the need for relevance. That's why I read (3) and (4) as implying (perhaps I should say 'implicating', but for now I'm going to go with the stronger word) a relevant connection between antecedent and consequent. Since that implication is, I presume, false in both cases, (3) and (4) are both false.
Alan,
It is always interesting and surprising to see how a test audience will respond to a sentence like (3). [ Alas, I have not actually tested with (3), but with similars.] When it is presented, first, without any indication of context, a good percentage of them react just as reacted. They search for, or simply assume, that there MUST be some connection in an unusual circumstance between a chess move and someone baking something. So they decline to condemn or label the sentence as “meaningless” because (a) it is grammatically unobjectionable and (b) they assume there is ( or at least could be ) some unusual context in which a speaker could sensibly utter it.
When we change the test and now specify a particular context for the utterance of (3)—so that it is now clear that they are being asked to evaluate a particular speaker’s utterance of (3) in a particular context—we usually cause a significant shift in their evaluations. Suppose we specify, for example, this background: Grand Master Larsen is being interviewed on camera about his loss this morning to the young Russian Karov. The interviewer questions Larson’s 32th move, when he declined a rook sacrifice that could have led to Karov losing his Queen in four moves. Larsen pauses and replies: “if I had sacrificed my rook at that point, Karov might or might not have a baked a cake.”
Speakers who had declined to call the contextless sentence (3) meaningless now tend to shift their position and condemn Larsen’s utterance as nonsense. [ But nonsense with a purpose, perhaps. Larsen has clearly refused or declined to answer the question, not by saying nothing, but by uttering a bit of jibberish. The utterance may still may its intended illocutionary and perlocutionary effect.]
As I said, I wish I could tell you that I’ve actually tested this example, ie., (3), but I’ve had this kind of result with similar examples. When you shift from contextless sentences to utterances with a clear context, speakers understand more clearly what you are asking them to evaluate: not whether a sentence is grammatical or has some possible use in some strange circumstance, but whether it has a meaning and a truth value in the given circumstance.
(4) –which I have actually used-- is something of an exception, but the exception tends to confirm the rule. Adding context doesn’t significantly increase the percentage of people who condemn (4), but that percentage was already very high. Even very imaginative people can’t fathom a possible situation in which there is a connection between the incommensurability of the square root of two and rain tomorrow.
Does it make sense to you to focus on utterances rather than contextless sentences, especially when we are interested in whether something a speaker has said has or lacks truth value?
Getting to the truth conditions for the utterance of conditionals is a BIG question—to which I have no satisfactory general answer-- but my rough conjecture is this. Speakers evaluate a conditional as true if they understand the kind of connection being asserted ( logical or lexical or causal or other) and believe that it actually obtains. They evaluate a conditional as false if they grasp the asserted connection and think it actually does not obtain. And they condemn an utterance when they cannot in the circumstances fathom any significant connection at all between antecedent and consequent. [ A speaker fails to understand the meaning of an English conditional if he proposes a conditional that does not at least allege the right kind of connection between supposition and consequent. ]
Post a Comment
Links to this post:
Create a Link
<< Home